Sample Bounds for Robust Multi-Object POMDP Planning via Rademacher Complexity

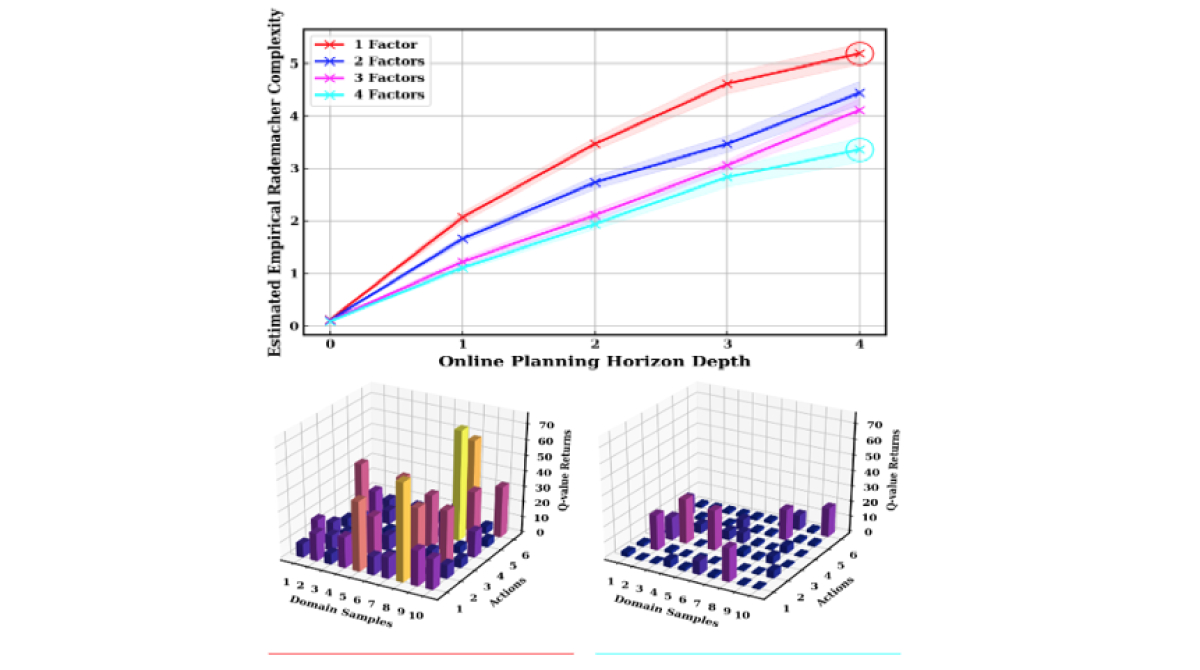
Object-based reasoning in real-world environments imposes a challenge: as the number of considered objects scale, planning becomes increasingly computationally intractable. In this paper, we derive general upper bounds on the number of samples for Q-value estimation in the context of object-based, online POMDP planning. Our bounds feature a novel application of Rademacher complexity for POMDPs, which comprises of two terms: a regularization term that penalizes complex POMDP models and a counting term that scales with the size of the POMDP problem. We compare bounds as we vary model factorization in terms of objects. We conclude by empirically validating our theoretical findings by demonstrating the advantage of belief factorization for supporting sample-efficient multi-object POMDP planning on a number of domains.